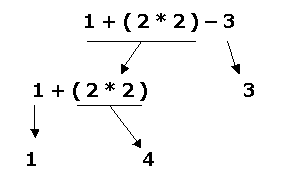
Internamente se busca el primer operador desde la derecha y se hacen los siguientes "razonamientos"
| 1 + ( 2 * 2 ) - 3 | "1 + ( 2 * 2 )" desconocido operado con 3 => Resolver "1 + ( 2 * 2 )" y operar luego |
| 1 + ( 2 * 2 ) | 1 operado con desconocido "( 2 * 2 )" => Resolver "(2 * 2)" y operar luego |
| 2 * 2 | 2 operado con 2 => Resolver = 4 |
| 1 + 4 | 1 operado con 4 => Resolver = 5 (aqui se ejecuta el "operar luego" que esta en la segunda linea) |
| 5 - 3 | 5 operado con 3 => Resolver = 2 (ahora el "operar luego" de la primera linea de la tabla) |
En definitva, lo unico que el programa sabe hacer son operaciones
basicas, como 2+2, 4*3, etc... Estas operaciones se
buscan de derecha
a izquierda en la ecuación y con un orden de prioridad: por
ejemplo, primero los signos
de + y - separan terminos, luego *, /, etc...
Para utilizar funciones como log, sen, cos, etc... no se como lo hancen otros programas, porque en su momento no encontré ideas en Internet para resolver este punto. En mi caso, lo que hice fue transformar esos nombres de funciones en operadores para volver a usar el codigo que ya tenia. Es decir, ademas de tener +,-,*,/, invente un operador @, de modo que lo que esta antes del operador identifica a la función a ejecutar y lo que esta después del operador es el valor de entrada para esa función.. Para aclarar este concepto vamos a un ejemplo: el usuario escribe "log 10" y el programa reemplaza una sola vez "log" por "1@", entonces queda "1@10". Cuando en la evaluacion encuentro la operacion @, busco de que funcion se trata. En este caso es la función "1", que es log (por ejemplo, la función exp podria ser 2, raiz cuadrada la 3, etc....). A continuación busco el valor de entrada, que es el segundo operando, en este caso 10 y ejecuto la funcion log de Basic para ese valor mediante un case.
Sin embargo, cuando estamos graficando, resolvemos la misma ecuación cientos de veces. Entonces, ¿porque no guardar el arbol de evaluación, en lugar de hacer uno diferente cada vez? Esto implica hacer una funcion de evaluación específica para graficar, que no es lo que esta en los libros. Lo que ocurre es que generalmente el programador usa codigo de evaluacion bajado de internet y le pone una interfaz grafica para obtener su graficador de funciones. De ahi en mas, simplemente se limitan a invocar el codigo de evaluacion para unos cuantos puntos del grafico, sustituyendo las variables por sus valores e invocando una y otra vez a la función de evaluación.
En mi caso, he realizado una especie de cache de terminos, operaciones y arbol de evaluación, que depende siempre de las variables x, p, etc... Sus valores no se sustuyen hasta el ultimo momento, de modo que se puedan volver a usar esos datos cuando cambian los valores de las variables. Es decir que dejo el arbol de evaluación armado para todos los valores de x, en lugar de generarlo una y otra vez, y además, como el orden se repite siempre, guardo el resultado de otros calculos y evaluaciones mediante el mismo principio.
Finalmente, al graficar, lo que se hace es evaluar la función para algunos puntos y unirlos, de modo que el usuario pueda ver el grafico en pantalla.
Con respecto al zoom, movimientos de pantalla, zoom a medida, etc... se trata basicamente de la aplicación de formulas de geometria analitica, en particular traslación de ejes y cambio de escalas. Al momento de realizar el grafico en pantalla se hace una conversión de los valores en numeros reales a "twips" o pixels, que son unidades de medida que se usan para medir distancias en pantalla. Para lograr el efecto zoom, basta con alterar esas relaciones, y para mover la pantalla se le suma o resta a los valores minimos y máximos del rango a graficar elegido inicialmente por el usuario.
Para utilizar funciones como log, sen, cos, etc... no se como lo hancen otros programas, porque en su momento no encontré ideas en Internet para resolver este punto. En mi caso, lo que hice fue transformar esos nombres de funciones en operadores para volver a usar el codigo que ya tenia. Es decir, ademas de tener +,-,*,/, invente un operador @, de modo que lo que esta antes del operador identifica a la función a ejecutar y lo que esta después del operador es el valor de entrada para esa función.. Para aclarar este concepto vamos a un ejemplo: el usuario escribe "log 10" y el programa reemplaza una sola vez "log" por "1@", entonces queda "1@10". Cuando en la evaluacion encuentro la operacion @, busco de que funcion se trata. En este caso es la función "1", que es log (por ejemplo, la función exp podria ser 2, raiz cuadrada la 3, etc....). A continuación busco el valor de entrada, que es el segundo operando, en este caso 10 y ejecuto la funcion log de Basic para ese valor mediante un case.
Sin embargo, cuando estamos graficando, resolvemos la misma ecuación cientos de veces. Entonces, ¿porque no guardar el arbol de evaluación, en lugar de hacer uno diferente cada vez? Esto implica hacer una funcion de evaluación específica para graficar, que no es lo que esta en los libros. Lo que ocurre es que generalmente el programador usa codigo de evaluacion bajado de internet y le pone una interfaz grafica para obtener su graficador de funciones. De ahi en mas, simplemente se limitan a invocar el codigo de evaluacion para unos cuantos puntos del grafico, sustituyendo las variables por sus valores e invocando una y otra vez a la función de evaluación.
En mi caso, he realizado una especie de cache de terminos, operaciones y arbol de evaluación, que depende siempre de las variables x, p, etc... Sus valores no se sustuyen hasta el ultimo momento, de modo que se puedan volver a usar esos datos cuando cambian los valores de las variables. Es decir que dejo el arbol de evaluación armado para todos los valores de x, en lugar de generarlo una y otra vez, y además, como el orden se repite siempre, guardo el resultado de otros calculos y evaluaciones mediante el mismo principio.
Finalmente, al graficar, lo que se hace es evaluar la función para algunos puntos y unirlos, de modo que el usuario pueda ver el grafico en pantalla.
Con respecto al zoom, movimientos de pantalla, zoom a medida, etc... se trata basicamente de la aplicación de formulas de geometria analitica, en particular traslación de ejes y cambio de escalas. Al momento de realizar el grafico en pantalla se hace una conversión de los valores en numeros reales a "twips" o pixels, que son unidades de medida que se usan para medir distancias en pantalla. Para lograr el efecto zoom, basta con alterar esas relaciones, y para mover la pantalla se le suma o resta a los valores minimos y máximos del rango a graficar elegido inicialmente por el usuario.