
Graficador matemático GDF |
GDF es un programa gratis que permite graficar cualquier función matemática en una variable, haces y conicas, sobre un sistema de coordenadas cartesiano con el propósito de verificar resultados de ejercicios como derivadas, signos, extremos relativos, límites, etc...
Para obtener mas información sobre el mismo consulte sus características en esta página.
Descargue gratuitamente el instalador para Windows (aproximadamente 2Mb) desde mi página de descargas.
 |
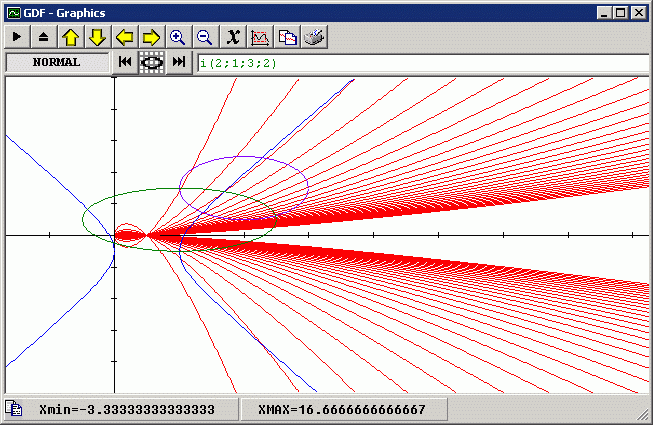
Grafica circunferencias, elipses, hipérbolas, haces de funciones, parábolas, etc... |
 |
Busca automáticamente máximos y mínimos en un gráfico proporcionando valores con una precisión de 15 dígitos en punto flotante. |
 |
Buscar gráficamente intersecciones entre dos o más funciones en pantalla, con la opción de asignar colores a cada una para identificarlas claramente. |
 |
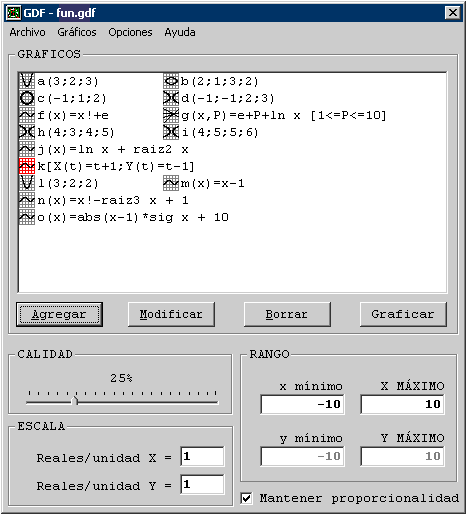
Se puede invocar una función de usuario desde otra y fijar valores de entrada para las funciones de usuario. Por ejemplo a(x)=x+1, b(x)=a(x)+1 ; c(x)=a(3)+1. Nota: No se puede anidar las funciones. Por ejemplo d(x)=a(b(x)) no es válido. |
 |
Muestra un icono con la tendencia (creciente/decreciente) al recorrer la función o curva. |
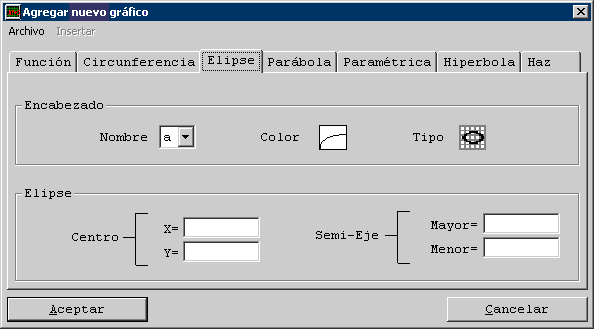
En esta ventana elija el tipo de curva a crear haciendo click en
la pestaña correspondiente (en la parte superior de la
ventana)
y a continuación complete los campos que aparecen en la
ficha.
Presione 'aceptar' y repita el proceso hasta agregar todas las curvas.
Finalmente presione 'graficar' en la ventana inicial.
Para colocar los paréntesis automáticamente: seleccione la parte de la ecuación a la que se le va a aplicar la función y haga click en el nombre de la función a insertar en el menú.
Por ejemplo si ha escrito x^2+x+1 y quiere obtener x^2+log (x+1): debe seleccionar "x+1" de la primer ecuación y hacer click en "logaritmo base 10" del menú insertar para que aparezca la segunda ecuación.
Funciones |
Operadores |
||
| abs | Valor absoluto | ! | Factorial |
| atn | Arcotangente | ^ | Potencia |
| cos | Coseno | * | Producto |
| exp | El número "e" elevado a una potencia | / | División |
| gamma | Función Gamma | \ | División entera (trunca el resultado) |
| inv | Inverso | - | Substracción |
| ln | Logaritmo neperiano | + | Adición |
| lngamma | Logatormo neperiano de gamma | Nota: Todas las
funciones trigonométricas
trabajan con grados. |
|
| log | Logaritmo base 10 | ||
| raiz2 | Raiz cuadrada | ||
| raiz3 | Raíz triple | ||
| sen | Seno | ||
| sig | Signo | ||
| tan | Tangente | ||
Estado de la licenciaPermiso vigenteEl permiso para la utilización de este producto se actualiza la primer semana de cada mes. Por mas información consulte la licencia del producto. |
Colabora con 5 euros para mejorar y mantener este programa. |
|
Si tienes una calculadora Casio: visita mi página web en la que publico programas gratis para resolver problemas de funciones, geometría analítica, consejos y juegos. |
|
| Como funciona GDF | Explica como funciona internamente GDF. |
| Autor | Información acerca del autor de este programa. |
| Errores reportados | Informe de evolución y errores corregidos de las versiones anteriores. |